Last week while rummaging through some old boxes I stumbled on a notebook with a curious algorithm for computing the cube root using a pocket calculator that has a square root button. For the cube root of 8 it goes:

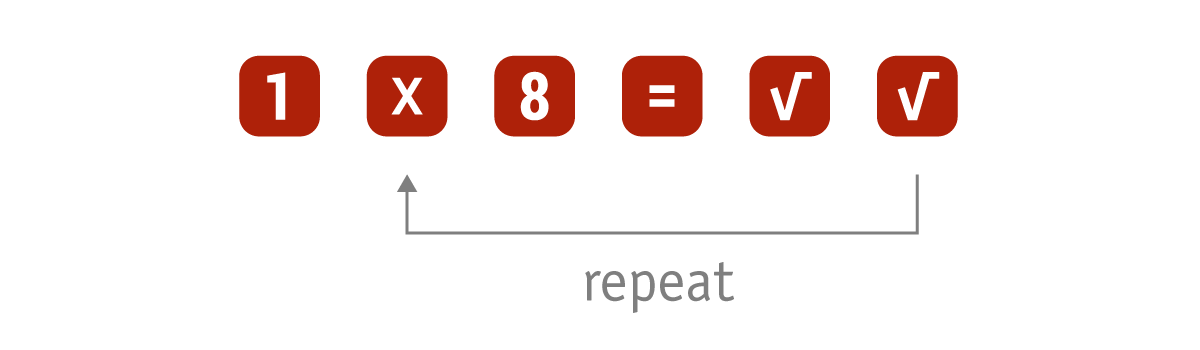
The result, 2, shows up after 10 iterations right after the two square roots. This algorithm is slower than Newton’s method and some of the other algorithms, but it has the advantage that it is fast to press. It takes 10 to 12 iterations for the algorithm to reach 6 digits of accuracy.

I stumbled on this algorithm by trial and error. My dad came back from a trip with a brand new Casio Mini Root M. I had seen electronic calculators in magazines, but this was the first one I had ever held. I played with it a lot.

Here is the cube root of 5 on the calculator (it was in the box and it still works)

What if we wanted a different root? Or even a different power? How does one compute an arbitrary power of a number using only the operations available on the Casio Mini Root? In most floating point libraries, powers are computed using the logarithm and exponential operators, but for fun I worked it out with the square root (the solution is in the Mathematica Notebook).